「2乗の平方根(ルート√)は絶対値となる」という結果を教えられて、なぜそうなるのか疑問に思う方も多いのではないでしょうか。
ここでは、なぜ2乗のルートが絶対値となるのかを考えたのちに、この性質を利用した問題を練習します。
(※なお、この内容は↓の動画でまとめていますので、合わせてご確認ください。)
なぜ2乗のルートは絶対値となるのか?

まず最初に、ルートの性質を復習しておきましょう。
例えば、\(\sqrt{5}\)とは、\(2\)乗して\(5\)になる数のことでした。
では、\((\sqrt{x})^2\)はどうなるでしょうか?
上記のルートの定義に照らせば、\(2\)乗して\(x\)になる数を\(2\)回かけるため、
$$(\sqrt{x})^2=x ・・・①$$
となるのは受け入れやすいと思います。
では次に、今回の本題である\(\sqrt{x^2}\)を考えていきます。
多くの方が間違えてしまうのは、\((\sqrt{x})^2\)の時と混同してしまい
$$\sqrt{x^2}=x$$
としてしまう事です。なぜ、これは誤りなのでしょうか?
具体的な例を考えると分かりやすいため、ここではまず\(x=+3\)としてみましょう。
\(x=+3\)のとき
①式の左辺は
\begin{eqnarray}
\sqrt{x^2}&=&\sqrt{3^2}\\
&=&3
\end{eqnarray}
となりますよね。
①式の右辺は、当然ですが
$$x=3$$
となります。つまり、①式は(左辺)=(右辺)が成立しています。
次に、\(x=-3\)の場合を考えてみたいと思います。
\(x=-3\)のとき
①式の左辺は
\begin{eqnarray}
\sqrt{x^2}&=&\sqrt{(-3)^2}\\
&=&\sqrt{(-1×3)^2}\\
&=&\sqrt{(-1)^2×3^2}\\
&=&\sqrt{3^2}\\
&=&3\\
\end{eqnarray}
となり、\(x\)にマイナスを入れたとしても、プラスになりました。
一方で、①式の右辺は
$$x=-3$$
となるため、マイナスになっています。これでは、①式の(左辺)=(右辺)が成立しませんよね。
なぜこのようなことになるかというと、左辺の\(x\)に負の数を入れても、結果的に正の数を入れた時と同じになるからです。
この「負の数を入れた場合、符号を逆にして正の数にする」というのは、まさに絶対値の性質そのものですよね。
つまり、冒頭の「なぜ2乗のルートは絶対値になるのか?」という問いの答えは、結果的に2乗のルートと絶対値の性質が全く同じだから、と言えます。
ここまでのまとめ
ここまでの過程を通じて
$$\sqrt{x^2}=|x|$$
となることが理解できたと思います。
絶対値記号を外す場合は、「絶対値記号の中身が正(プラス)であればそのまま外に、中身が負(マイナス)であれば符号を逆にして出す」と考えることができました。
よって
$$\sqrt{x^2}=|x|=\left\{
\begin{array}\
x & (x \ge 0) \\
-x & (x < 0)
\end{array}
\right.
$$
となることを理解して頂けたのではないでしょうか。
「2乗のルートは絶対値!」という言葉を繰り返して、身体に覚えこませてしまいましょう!
「2乗のルート=絶対値」の練習問題
最後に、具体的な問題で練習しておきましょう。この2乗のルートを含んだ問題は、大学入試試験にも頻出です。
【問題1】ルートの付かない形にせよ。
$$\sqrt{x^2y^2}\hspace{10pt}(x>0,y<0)$$
【問題2】ルートの付かない形にせよ。
$$\sqrt{x^2-2x+1}+\sqrt{x^2+6x+9}$$
なお、絶対値の場合分けをする時としない時の見分け方については、次の記事でまとめていますので、合わせてご確認ください。


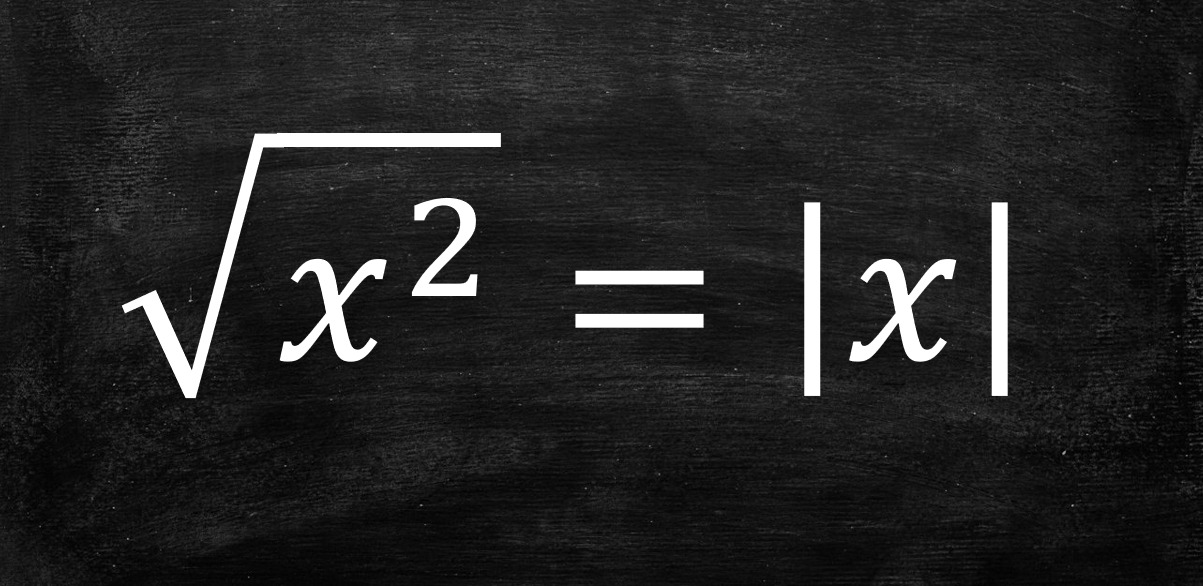
コメント