絶対値を含む問題において、場合分けをする時としない時にはどのような違いがあるのか分からず、困ってしまうことは無いでしょうか。
この記事を読んで頂くことで、絶対値の場合分けをする時としない時の判別ができるようになります。
なお、この場合分けの内容も含めて、動画でも詳しく解説していますので、合わせてご覧ください。(動画の26:19から場合分けをする時しない時について説明しています)
絶対値の場合分けをしなくても解ける2パターン

まず理解しておきたいことは、「絶対値を含む問題が出題された際には、場合分けが基本」ということです。
この基本は、場合分けをせず解く方法を学ぶ時にこそ、再確認したいポイントです。
このポイントを理解したうえで、絶対値の場合分けをしなくても解ける2つのパターンを紹介します。
パターン①:絶対値と定数項が両辺に分かれた形
左辺が絶対値のみであり、右辺が\(x\)等の変数を含まない定数項の場合、場合分けをしなくても簡単に解くことができます。
\(A\)を1次式、\(B\)を定数項とすると
$$|A|=B$$
の場合には、
$$A=\pm B$$
のように、\(\pm\)を付けて絶対値を外すことができます。
なぜこのように絶対値を外す事ができるのでしょうか?
まず、絶対値の定義が「原点からの距離」であることから、\(|A|=B\)の意味は、\(A\)は原点\(0\)から\(B\)だけ離れた場所という事ができます。
具体的な例で考えてみましょう。
例えば\(|x|=2\)は、\(x\)が原点から\(2\)離れた場所に存在する、という意味です。
原点からは、正の方向にも負の方向にも離れて良いので、図示すれば次のようになるはずです。
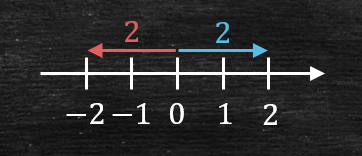
この図から分かるように、\(x\)は正の方向(青矢印)に進んだプラス\(2\)の点、及び負の方向(赤矢印)に進んだマイナス\(2\)の点の2ヵ所に存在するはずです。
このように考えれば、\(x\)が\(\pm 2\)になる、という結果を受け入れやすいのではないでしょうか。
結果として、\(\pm\)を付けて絶対値を外す事が可能になるというわけです。
この\(|x|=2\)の例でも、\(x\)が\(0\)以上の時と\(0\)以下の時で場合分けをして考える事もできますが、\(\pm\)を付けて絶対値を外せば1行で答えに辿り着けるため、圧倒的に早いです。
具体的な問題で練習しておきましょう。
【問題1】次の方程式を解け。
$$\left|\frac{1}{2}x\right|=4$$
【問題2】次の方程式を解け。
$$|x+2|=2$$
ここで1つ注意すべき点を解説します。この\(\pm\)を付けて絶対値を外す方法に慣れると、次のような方程式を解くときに、
$$|2x+1|=x$$
以下のように解いていってしまう場合があります。
$$2x+1=\pm x$$
このまま、計算を進めていって、\(x\)がプラスの時には\(x=-1\)、\(x\)がマイナスの時には\(x=-\frac{1}{3}\)としてしまうのは、絶対値の外し方として間違っています。
仮に\(\pm x\)として絶対値を外す場合には、\(x\ge0\)の条件を付けなければなりません。
そのため、この問題ではやはり、絶対値の中身の正負で場合分けをして解くという基本に立ち返る必要があります。
(この問題の本当の答えは、解無し、となります。)
パターン②:両辺が絶対値だけの形
両辺がそれぞれ絶対値だけになっている場合も、場合分けをせず解く事が可能です。
両辺が絶対値だけであればどちらもプラスなので、両辺を2乗しても同値である、という性質を利用します。
\(A\)を\(n\)次式、\(B\)を\(m\)次式もしくは定数項とすると
$$|A|=|B|$$
の場合には、両辺を2乗して
$$|A|^2=|B|^2$$
$$A^2=B^2$$
と絶対値を外す事が可能です。
このパターンも、具体的な問題で練習しておきましょう。
【問題3】次の方程式を解け。
$$|3x-1|=|x-3|$$
【問題4】次の方程式を解け。
$$|x^2-4|=3|x|$$
特にこの問題4は、仮に場合分けして解くとすると、4つに場合分けする必要があり、計算が大変になります。
そういった意味で、両辺が絶対値だけの時には両辺を2乗する、という手法を知っておくことは、大きな武器になると思います。
絶対値の場合分けが必要なパターン

では、絶対値の問題で場合分けする時とは、どのような時なのでしょうか?
それはこれまで説明した、\(\pm\)を付けて絶対値を外す(パターン①)、両辺を2乗(パターン②)のどちらも用いる事のできない問題です。
つまり、絶対値の問題が出題された際には、まずパターン①、②の式の形になっているか確認し、それ以外は全て場合分けをして解く、と覚えておくとよいと思います。
このパターン①、②に当てはまらない問題は「絶対値の中身の正負で場合分け」しましょう。
ここでは、場合分けしなければ解く事のできない問題も練習しておきましょう。
【問題5】次の方程式を解け。
$$|x-1|+2|x-3|=4$$
絶対値の場合分け|まとめ
この記事では、絶対値の場合分けが必要ない2パターンと、それ以外のパターンにおける3つの解法を紹介しました。
絶対値の場合分けをする時としない時について、マスターして頂ければ幸いです。


コメント